Someone I Would Like to Argue With

I’ve been reading an interview with James Lovelock, famous largely for the Gaia Hypothesis, which always looked a bit nutty to me. He sounds like an interesting man. Unlike most people in public controversies, he is willing to admit that he was wrong:

The Revenge of Gaia was over the top, but we were all so taken in by the perfect correlation between temperature and CO2 in the ice-core analyses [from the ice-sheets of Greenland and Antarctica, studied since the 1980s]. You could draw a straight line relating temperature and CO2, and it was such a temptation for everyone to say, “Well, with CO2 rising we can say in such and such a year it will be this hot.” It was a mistake we all made.

We shouldn’t have forgotten that the system has a lot of inertia and we’re not going to shift it very quickly. The thing we’ve all forgotten is the heat storage of the ocean — it’s a thousand times greater than the atmosphere and the surface. You can’t change that very rapidly.

He is dismissive of pop-catastrophism, as in the case of Fukushima, pointing out that “Twenty-six thousand people were killed by the magnitude-9 earthquake and tsunami [that caused the nuclear meltdown], and how many are known to have been killed by the nuclear accident? None.”

He is skeptical about the chance of any political solution to climate change, arguing for adaptation rather than prevention, and, if I interpret him correctly, recognizing that getting the English to save England is a more viable strategy than getting them to try to help save the world. And he recognizes that the future is very uncertain. Responding to a question about what the next 100 years will be like with:

That’s impossible to answer. All I can say is that it will be nowhere as near as bad as the worst-case scenario.

I expect that I would disagree with a fair number of his views, but he sounds like someone it would be fun to argue with.

Is the IPCC High Emissions Scenario Impossible?

A commenter here a while back argued that RCP 8.5, the highest emission scenario in the current IPCC report, is impossible, because it requires more coal than is available to be mined. I recently came across a more detailed version of that argument in a published piece by David Rutledge, a Caltech professor.

The argument is straightforward. Estimates of coal reserves are much more reliable than estimates of reserves of oil and gas, coal being a solid. Such  estimates have been made for more than a century and actual quantities mined have, so far, been consistent with them. In particular:

for coal the pattern has been that countries produce only a small fraction of their early reserves, and then late in the production cycle the reserves drop to match the coal at the last working mines. This pattern is seen in the UK (cumulative production of 19% of early reserves), Pennsylvania anthracite (42%), the Ruhr Valley (14%), France and Belgium (23%), and Japan and South Korea (21%). This means that the reserves criteria have been too optimistic, but it also means that world coal reserves are a good upper bound on future production.

By the author's calculation, RCP 8.5 requires the world to consume 200% of total coal reserves by 2100, 700% by 2500. If he is correct, it follows that RCP 8.5 ought not to be included in the IPCC graphs showing possible future climate change and that maximum values of temperature change or sea level rise ought not to include the values it would imply.

I have two questions for readers:

1. Can anyone point at a serious mistake in the argument? Does it misstate the amount of coal consumption implied by RCP 8.5, the size of coal reserves as currently estimated or the reasons to think that current estimates represent a reasonable upper bound?

2. Is there anyone here otherwise inclined to support the IPCC who, having looked at this argument, agrees that the inclusion of RCP 8.5 in the report is fraudulent, an attempt to make risks of future warming look worse than they actually are?

AGW, Considered as a Black Swan

In my previous post I took issue with Lovejoy's claim to show, by statistical analysis of global temperature data since 1500, that the probability that natural processes would produce the amount of warming observed in the period 1880 to 2008 was less, probably much less, than one in a hundred. My complaint was not with his conclusion, which might well be true, but with his argument.

In order to calculate the probability that what happened would happen as a result of natural causes of temperature change, Lovejoy needed a probability distribution showing what the probability was of a natural cause producing any given temperature change. He could estimate that distribution by looking at changes over the period from 1500 to 1880 on the (plausible) assumption that humans had little effect on global temperature over that period. But that data could not tell him the probability distribution for events rare enough to be unlikely to show up in his data, for instance some cause of warming that occurred with an annual probability of only .001.

His solution to that problem was to assume a probability distribution, more precisely a range of possible distributions, fit it with the data he had and deduce from it the probability of the rare large events that might have provided a natural cause for 20th century warming. That makes sense if those events are a result of the same processes as the more frequent events, just less likely versions of them—just as flipping a coin and getting eight heads in a row is a result of the same processes that give you four, five, or six heads in a row. But it makes no sense if there are rare large events that are produced by some entirely different process, one whose probability the observed events tell us nothing about—if, for instance, you got four heads in a row by sheer luck, forty heads in a row because someone had slipped you a two headed coin. The forty heads, or the hypothetical rare cause of large warming, would be a black swan, an event sufficiently rare that it had not been observed and so was left out of the calculation.

It occurred to me, after considering a response by Lovejoy and a comment on the Google+ version of my post, that not only was such a black swan event possible in the context of climate, one had occurred. AGW itself is a black swan, a cause of rapid warming whose probability cannot be deduced by looking at the distribution of climate change from the period 1500 to 1880.

If the point is not clear, imagine that Lovejoy wrote his article in 1880. Since warming due to human activity had not yet occurred, there would be no reason for him to distinguish between causes of warming and natural causes of warming. He would interpret the results of his calculations as showing that the probability of warming by a degree C over the next 128 years was less, probably much less, than .01. He would be assuming away the possibility of some cause of substantial warming independent of the causes of past warming, one whose probability could not be predicted from their probability distribution.

That cause being, of course, greenhouse gases produced by human action.

Two Problems With the 1% Claim

A number of news stories claim that a recent paper by Lovejoy proves that the probability that the warming of the past century is entirely due to natural causes is less than one percent. I find the conclusion plausible enough, but, so far as I can tell, there is no way that it can be derived in the way Lovejoy is said to have derived it.

The first problem, probably the fault of the reporters not of Lovejoy himself, is the misinterpretation of what the confidence result produced by classical statistics means. If you analyze a body of data and reject the null hypothesis at the .01 level, that means that if the null hypothesis is true, the probability that the evidence against it would be as strong as it is is less than .01—the probability of the evidence conditional on the null hypothesis. That does not imply that the probability that the null hypothesis is true given that the evidence against it is that strong is less than .01—the probability of the null hypothesis conditional on the evidence. The two sound similar but are in fact entirely different. 

My standard example is to imagine that you pull a coin out of your pocket, toss it without inspecting it, and get heads twice. The null hypothesis is that it is a fair coin, the alternative hypothesis that it is a double headed coin. The chance of getting two heads if it is a fair coin is only .25. It does not follow that, after getting two heads, you should conclude that the probability is .75 that the coin is double headed. For previous discussions of this issue see this one in the contest of World of Warcraft and this in the context of DNA analysis of mummies.

The second problem is that, so far as I can tell, there is no way Lovejoy could have calculated the probability that natural processes would produce 20th century warming from the data he was using, which consisted of a reconstruction of world temperature from 1500 to the present. The paper is sufficiently complicated so that I may be misinterpreting it, but I think his procedure went essentially as follows:

Assume that changes in global temperature prior to 1880 were due to random natural causes. Use the data from 1500 to 1875 to estimate the probability distribution of natural variation in global temperature. Given that distribution, calculate the probability that natural variation would produce as much warming from 1880 to 2008 as occurred. That probability is less than .01. Hence reject the assumption that warming from 1880 on was entirely due to natural causes at the .01 level.

The problem with this procedure is that data from 1500 on can only give information on random natural processes whose annual probability is high enough so that their effect can be observed and their probability calculated within that time span. Suppose there is some natural process capable of causing a global temperature rise of one degree C in a century whose annual probability is less than .001. The odds are greater than even that it will not occur even once in Lovejoy's data. Hence he has no way of estimating the probability that such a process exists. The existence of such a process would provide an explanation of 20th century warming that does not involve human action. So he cannot estimate, from his data, how likely it is that natural processes would have produced observed warming, which is what he is claiming to do. 20th century warming would, in that case, be what Taleb refers to as a Black Swan event. If one swan in a thousand is black, the observer looks at five hundred swans, finds all of them white, and concludes, incorrectly, that the probability of a black swan is zero.

How does Lovejoy solve that problem? If I correctly read the paper, the answer is:

Stated succinctly, our statistical hypothesis on the natural variability is that its extreme probabilities ... are bracketed by a modified Gaussian...

In other words, he is simply assuming a shape for the probability distribution of natural events that affect global climate. Given that assumed shape, he can use data on the part of the distribution he does observe to deduce the part he does not observe. But he has no way of testing the hypothesis, since it is a hypothesis about a part of the curve for which he has no data.

If I am correctly reading the paper—readers of this post are welcome to correct me if they think I am not—that means that Lovejoy has not only not proved what reporters think he has, he has not proved what he thinks he has either. A correct description of his result would be that the probability that natural processes would produce observed warming, conditional on his assumption about the shape of the probability distribution for natural processes that affect global temperature, is less than .01.

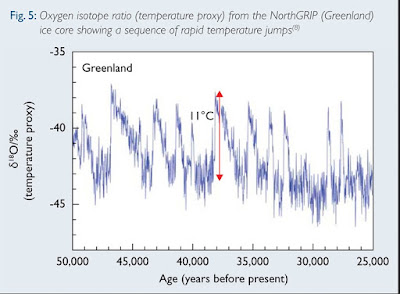
One obvious question is whether this problem matters, whether, on the basis of data other than what went into Lovejoy's paper, one can rule out the possibility of natural events capable of causing rapid warming that occur too infrequently for their probability to be deduced from the past five hundred years of data. I think the answer is that we cannot. The figure below is temperature data deduced from a Greenland ice core. It shows periods of rapid warming, some much more rapid than what we observed in the 20th century, occurring at intervals of several thousand years. During one of them, "The temperature increased by more than 10°C within 40 years." The temperature shown is local not global—we do not have the sort of paleoclimate reconstructions that would be needed to spot similar episodes on a global scale. But the fact that there are natural sources of very rapid local warming with annual frequency below .001 is an argument against ruling out the possibility that such sources exist for global warming as well.

In my next post, I pointed out that not only was it possible that there existed a low probability process capable of producing rapid warming whose cause and hence  probability was independent of the higher probability processes Lovejoy observed, it appears to have actually happened—certainly Lovejoy believes it did. AGW itself is a black swan in precisely the sense discussed above.

A Few More Bits from the IPCC Fifth Assessment Report

(Chapter 10, Second draft)

An assessment of the observational evidence indicates that the AR4 conclusions regarding global increasing trends in hydrological droughts since the 1970s are no longer supported. ... we conclude there is low confidence in attributing changes in drought over global land since the mid-20th century to human influence.

Contrast that to all the claims blaming the current California drought on global warming.

The average global cyclone activity is expected to change little under moderate greenhouse gas forcing

Globally, there is low confidence in any long term increases in tropical cyclone activity (Section 2.6.3) and low confidence in attributing global changes to any particular cause.

Or, in other words, Chris Landsea was right.

Anthropogenic warming remains a relatively small contributor to the overall magnitude of any individual short-term event because its magnitude is small relative to natural random weather variability on short time scales. Because of this random variability, weather events continue to occur that have been made less likely by human influence on climate, such as extreme winter cold events ...

Contrast the final sentence to occasional claims that recent unusual cold is evidence for, not against, "climate change."
 
The chapter also contains a graph showing estimates of northern hemisphere temperature over the past 1200 years. It appears from the green lines, due to Michael Mann of hockey stick fame, that the medieval warm period is back, with a peak close to current temperature. 

 

Ocean Warming Data

I have several times seen the claim that, despite the apparent pause in surface temperatures, global warming is actually going faster than ever, with the missing heat in the ocean. So far I have seen no support for that claim. I did, however, recently come across an article discussing global heat content changes and problems in estimating them that contains an interesting graph.

As best I can tell, the different lines represent different ways of estimating the values, given the data limitations, with data becoming available later for the deeper depths; the vertical lines show, for each depth, the date when global coverage reached 50%. So the bottom graph is the best in terms of how deep it goes, the worst in quality of the data.

The  pattern seems pretty clear. Slow warming until about 1996, faster from then until about 2004, slower to zero warming thereafter.

Another Critic of Cook et. al. 2013

Readers will be familiar with my critique of Cook et al. 2013, an article widely cited as showing that 97% of climate researchers support "the consensus position." I have just come across a much more detailed criticism of the paper on other grounds, by someone much more extensively involved in climate issues than I am.

Climate Nuts vs the IPCC

In one recent climate thread on Google+, I was informed, by three different people, that global warming would:

Create two billion climate refugees

Flood most of the world's large cities

Destroy civilization.

The simplest rebuttal to such claims is the latest IPCC report. The IPCC, after all, is doing its best to persuade people to support action to slow global warming, so unlikely to minimize the problem. But if you look not at the rhetoric but at the factual claims, the impending climate catastrophe looks like a wet firecracker. For instance:

There is no evidence that surface water and groundwater drought frequency has changed over the last few decades, although impacts of drought have increased mostly due to increased water demand.

Economic losses due to extreme weather events have increased globally, mostly due to increase in wealth and exposure, with a possible influence of climate change (low confidence in attribution to climate change).

Some low-lying developing countries and small island states are expected to face very high impacts that, in some cases, could have associated damage and adaptation costs of several percentage points of GDP.

... most recent observed terrestrial-species extinctions have not been attributed to recent climate change, despite some speculative efforts (high confidence).

With these recognized limitations, the incomplete estimates of global annual economic losses for additional temperature increases of ~2°C are between 0.2 and 2.0% of income ... .

Oddly enough, precisely the same evidence can be used against nuts on the other end of the spectrum, such as the gentleman in one thread who claimed that the IPCC had a budget in excess of twelve billion dollars. Pointing out to him that the actual budget, available on the web, came to about eleven million dollars had no effect. If, as he confidently believes, the IPCC is a massive fraud, inventing global warming out of thin air for its own sinister purposes, why should I be so naive as to believe their account of their budget? Pointing to webbed data on global temperature, which has increased by about  one degree C since 1910, would be no more effective, since he can, and probably would, claim that the data are fake. 

What he cannot explain away so easily is the modesty of the IPCC's claims. If, as he (correctly) believes, they are trying to scare people into doing something about global warming and if, as he (incorrectly) believes, they are unconstrained by actual evidence and science, why don't they tell a better story? Two degrees of warming over the next 86 years, a foot or two of sea level rise, are not very impressive threats, despite all the rhetorical efforts of the IPCC and its supporters. Why don't they make it ten degrees and ten feet? Twenty feet? A hundred feet? Why don't they tell something closer to the story that their nuttier supporters want to believe?